
High-throughput technologies changed the face of biology and medicine within the last two decades. This connection allows to shed light on the well-known heterogeneity of statistical estimation methods for inferring gene regulatory networks and provides an explanation for the difficulties inferring molecular interactions between highly connected genes. Second, we connect these results, obtained from a probabilistic perspective, to statistical results of studies aiming to estimate gene regulatory networks from biological data. We study local and global characteristics of these covariance matrices, and derived concentration/partial correlation matrices. Such covariance matrices are playing a pivotal role in designing novel statistical methods for high-dimensional biological data, because they allow to define Gaussian graphical models (GGM) for the simulation of realistic data including their correlation structure. First, we investigate three methods for generating constrained covariance matrices with a biologically realistic structure.
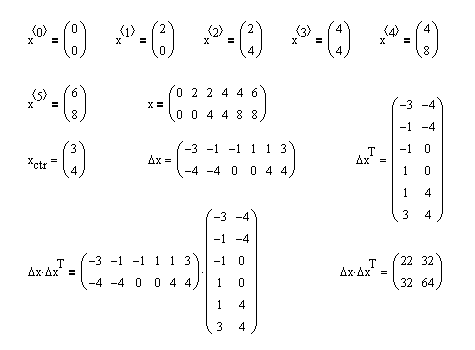
This fact is particularly well-known for gene expression data, because there is a sufficient number of large-scale data sets available that are amenable for a sensible statistical analysis confirming this assertion. High-dimensional data from molecular biology possess an intricate correlation structure that is imposed by the molecular interactions between genes and their products forming various different types of gene networks.

In this section, that convention leads to notation that is a bit nonstandard, since the objects that we will be dealing with are vectors and matrices. We will follow our usual convention of denoting random variables by upper case letters and nonrandom variables and constants by lower case letters. Also we assume that expected values of real-valued random variables that we reference exist as real numbers, although extensions to cases where expected values are \(\infty\) or \(-\infty\) are straightforward, as long as we avoid the dreaded indeterminate form \(\infty - \infty\). We assume that the various indices \( m, \, n, p, k \) that occur in this section are positive integers. This section requires some prerequisite knowledge of linear algebra.
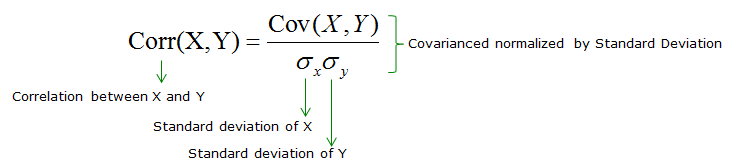
These topics are somewhat specialized, but are particularly important in multivariate statistical models and for the multivariate normal distribution. The main purpose of this section is a discussion of expected value and covariance for random matrices and vectors.


 0 kommentar(er)
0 kommentar(er)
